
統計學到底有多重要?
在回答資料分析入門要具備什麼樣的能力的問題中,我經常提到統計學知識,統計學是一種利用數學理論來進行資料分析的技術,通過統計學我們可以用更富有資訊驅動力和針對性的方式對資料進行操作。
在資料分析工作中,利用統計學,我們可以更深入、更細緻地觀察資料是如何進行精確組織的,並且基於這種組織結構確定資料分析的方法,來獲取更多的資訊。今天給大家介紹資料分析中常用的五個統計基本概念。
統計學——特徵
特徵統計可能是資料科學中最常用的統計學概念。它是你在研究資料集時經常使用的統計技術,包括偏差、方差、平均值、中位數、百分數等等。理解特徵統計並且在程式碼中實現都是非常容易的。請看下圖:

上圖中,中間的直線表示資料的中位數。中位數用在平均值上,因為它對異常值更具有魯棒性。第一個四分位數本質上是第二十五百分位數,即資料中的25%要低於該值。第三個四分位數是第七十五百分位數,即資料中的75%要低於該值。而最大值和最小值表示該資料範圍的上下兩端。
箱形圖很好地說明了基本統計特徵的作用:
- 當箱形圖很短時,就意味著很多資料點是相似的,因為很多值是在一個很小的範圍內分佈;
- 當箱形圖較高時,就意味著大部分的資料點之間的差異很大,因為這些值分佈的很廣;
- 如果中位數接近了底部,那麼大部分的資料具有較低的值。如果中位數比較接近頂部,那麼大多數的資料具有更高的值。基本上,如果中位線不在框的中間,那麼就表明了是偏斜資料;
- 如果框上下兩邊的線很長表示資料具有很高的標準偏差和方差,意味著這些值被分散了,並且變化非常大。如果在框的一邊有長線,另一邊的不長,那麼資料可能只在一個方向上變化很大
統計學——概率分佈
我們可以將概率定義為一些事件將要發生的可能性大小,以百分數來表示。在資料科學領域中,這通常被量化到0到1的區間範圍內,其中0表示事件確定不會發生,而1表示事件確定會發生。那麼,概率分佈就是表示所有可能值出現的機率的函數。請看下圖:

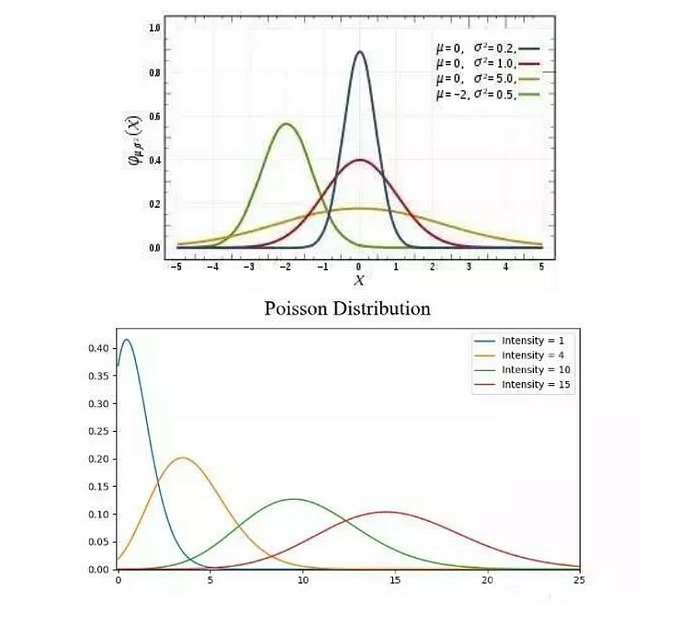
常見的概率分佈,均勻分佈(上)、正態分佈(中間)、泊松分佈(下):
- 均勻分佈是其中最基本的概率分佈方式。它有一個只出現在一定範圍內的值,而在該範圍之外的都是0。我們也可以把它考慮為是一個具有兩個分類的變數:0或另一個值。分類變數可能具有除0之外的多個值,但我們仍然可以將其視覺化為多個均勻分佈的分段函數
- 正態分佈,通常也稱為高斯分佈,具體是由它的平均值和標準偏差來定義的。平均值是在空間上來回變化位置進行分佈的,而標準偏差控制著它的分佈擴散範圍。與其它的分佈方式的主要區別在於,在所有方向上標準偏差是相同的。因此,通過高斯分佈,我們知道資料集的平均值以及資料的擴散分佈,即它在比較廣的範圍上擴充套件,還是主要圍繞在少數幾個值附近集中分佈。
- 泊松分佈與正態分佈相似,但存在偏斜率。象正態分佈一樣,在偏斜度值較低的情況下,泊松分佈在各個方向上具有相對均勻的擴散。但是,當偏斜度值非常大的時候,我們的資料在不同方向上的擴散將會是不同的。在一個方向上,資料的擴散程度非常高,而在另一個方向上,擴散的程度則非常低。
如果遇到一個高斯分佈,那麼我們知道有很多演算法,在預設情況下高思分佈將會被執行地很好,因此首先應該找到那些演算法。如果是泊松分佈,我們必須要特別謹慎,選擇一個在空間擴充套件上對變化要有很好魯棒性的演算法。
統計學——降維
降維這個術語可以很直觀的理解,意思是降低一個數據集的維數。在資料科學中,這是特徵變數的數量。請看下圖:

上圖中的立方體表示我們的資料集,它有3個維度,總共1000個點。以現在的計算能力,計算1000個點很容易,但如果更大的規模,就會遇到麻煩了。然而,僅僅從二維的角度來看我們的資料,比如從立方體一側的角度,可以看到劃分所有的顏色是很容易的。
通過降維,我們將3D資料展現到2D平面上,這有效地把我們需要計算的點的數量減少到100個,大大節省了計算量。
另一種方式是我們可以通過特徵剪枝來減少維數。利用這種方法,我們刪除任何所看到的特徵對分析都不重要。
例如,在研究資料集之後,我們可能會發現,在10個特徵中,有7個特徵與輸出具有很高的相關性,而其它3個則具有非常低的相關性。那麼,這3個低相關性的特徵可能不值得計算,我們可能只是能在不影響輸出的情況下將它們從分析中去掉。
用於降維的最常見的統計技術是PCA,它本質上建立了特徵的向量表示,表明了它們對輸出的重要性,即相關性。PCA可以用來進行上述兩種降維方式的操作。
統計學——過取樣和欠取樣
過取樣和欠取樣是用於分類問題的技術。例如,我們有1種分類的2000個樣本,但第2種分類只有200個樣本。這將拋開我們嘗試和使用的許多機器學習技術來給資料建模並進行預測。那麼,過取樣和欠取樣可以應對這種情況。請看下圖:

在上面圖中的左右兩側,藍色分類比橙色分類有更多的樣本。在這種情況下,我們有2個預處理選擇,可以幫助機器學習模型進行訓練。
欠取樣意味著我們將只從樣本多的分類中選擇一些資料,而儘量多的使用樣本少的分類樣本。這種選擇應該是為了保持分類的概率分佈。我們只是通過更少的抽樣來讓資料集更均衡。
過取樣意味著我們將要建立少數分類的副本,以便具有與多數分類相同的樣本數量。副本將被製作成保持少數分類的分佈。我們只是在沒有獲得更多資料的情況下讓資料集更加均衡。
統計學——貝葉斯統計
完全理解為什麼在我們使用貝葉斯統計的時候,要求首先理解頻率統計失敗的地方。大多數人在聽到“概率”這個詞的時候,頻率統計是首先想到的統計類型。它涉及應用一些數學理論來分析事件發生的概率,明確地說,我們唯一計算的資料是先驗資料(prior data)。

假設我給了你一個骰子,問你擲出6點的機率是多少,大多數人都會說是六分之一。
但是,如果有人給你個特定的骰子總能擲出6個點呢?因為頻率分析僅僅考慮之前的資料,而給你作弊的骰子的因素並沒有被考慮進去。
貝葉斯統計確實考慮了這一點,我們可以通過貝葉斯法則來進行說明:
在方程中的概率P(H)基本上是我們的頻率分析,給定之前的關於事件發生概率的資料。方程中的P(E|H)稱為可能性,根據頻率分析得到的資訊,實質上是現象正確的概率。
例如,如果你要擲骰子10000次,並且前1000次全部擲出了6個點,那麼你會非常自信地認為是骰子作弊了。如果頻率分析做的非常好的話,那麼我們會非常自信地確定,猜測6個點是正確的。同時,如果骰子作弊是真的,或者不是基於其自身的先驗概率和頻率分析的,我們也會考慮作弊的因素。
正如你從方程式中看到的,貝葉斯統計把一切因素都考慮在內了。當你覺得之前的資料不能很好地代表未來的資料和結果的時候,就應該使用貝葉斯統計方法。
回顧系列文:
我是「數據分析那些事」。常年分享數據分析乾貨,不定期分享好用的職場技能工具。按贊我的臉書,私訊我10,送你十週入門數據分析電子書唷!期待你與我的互動!
